Video and reference

Please refer to this paper when you cite any work from this blog:
Semi-autonomous navigation for robot assisted tele-echography using generalized shape models and co-registered RGB-D cameras
Lin Zhang and Su-Lin Lee and Guang-Zhong Yang and Mylonas, G.P.
Intelligent Robots and Systems (IROS 2014), 2014 IEEE/RSJ International Conference on

Experiment on effect of differently cropped shape on SSM

In order to achieve better validation result, I am trying to use the shape models that were cropped differently according to target object.
As the back of subject cannot been seen by both Kinects and the plastic torso is rigid and not as same as human torso, I tried to use shapes whose back have been cropped (shown in Figure 1).

Figure 1 Torso shape model (no head, legs, arms and back)

For real human subject, since the head and arms are required (no head nor arms for the plastic torso), I remain the head and part of arm for shape model training (shown in Figure 2).

Figure 2 Torso shape model (no legs, part arms and no back)

Colour Point Cloud detection and extraction based on HSV colour space

In order to register the Kinects with KUKA robot which is fixed on a optical table, I use three color markers whose position is known within KUKA coordinate system.
Here is a snapshot of the markers:

Figure 1 Three colour markers with three different colours (R, G, B)

As shown in the Figure 1, three markers are painted as red, green and blue respectively. These three markers are read as RGB point cloud from the Kinect after combining depth image with colour image. However, similar colours describing by RGB components are not easy to distinguish with each other if environment illumination is variant from time to time, therefore, difficult to choose thresholds of colour components for point cloud filtering.

To address above weakness, instead of using RGB colour space, we can use HSV (Hue, Saturation and Value) space for colour representation. The following figure shows that how value of the hue, saturation and value components can be changed.
Hue: 0 - 360 (°)
Saturation: 0 - 100 (%)
Value: 0 - 100 (%)

Figure 2 HSV colour space can be visualised as a single cone [1]

For my markers, I used following conditions to extract them out:
RED: 
if (HSV_map_->points[i].s <= 0.2 || HSV_map_->points[i].v <= 0.2)
// Not target colour
if (HSV_map_->points[i].s <= 0.4 && HSV_map_->points[i].v <= 0.4)
// Not target colour
if (HSV_map_->points[i].h >= 350 || HSV_map_->points[i].h < 10)
// Can be target colour

GREEN:
if (HSV_map_->points[i].s <= 0.3 || HSV_map_->points[i].v <= 0.3)
// Not target colour
if (HSV_map_->points[i].h >= 100 && HSV_map_->points[i].h < 140)
// Can be target colour

BLUE:
if (HSV_map_->points[i].s <= 0.3 || HSV_map_->points[i].v <= 0.3)
// Not target colour
if (HSV_map_->points[i].h >= 220 && HSV_map_->points[i].h < 260)
// Can be target colour

After the potential target colour points are extracted, we need to filter out the outliers caused by noises. Here we need to have an assumption that the marker is the largest objects (most number of points) with that specific colour within field of view. Hence, it is able to use Euclidean Cluster Extraction algorithm implemented in PCL (link) to get the largest cluster which hopefully is our marker. Since the marker has circular shape, mean value of the extracted points can be treated as centre of the marker.

Based on the calculation so far, it is able to get position three points in 3D space in both coordinates. The transformation (only rotation + rotation) between two coordinates is able to calculated using PCL function pcl::registration::TransformationEstimationSVD::estimateRigidTransformation (link).


Results:

Experiment 1: Three markers are placed on a flat table. First coordinate is same as Kinect coordinate. The origin of second coordinate is defined as centre of the red marker while red-green is x-axis and red-blue is y axis. Since right hand coordinate was used, the z axis of the second coordinate is upward out of table. The lengths of red-green line and red-blue line are both 30 cm measured by ruler.

Figure 3 Result of experiment 1

From the Figure 3, we can see that the Kinect coordinate was almost perfectly aligned with the coordinate defined by ourself.

Experiment 2: In this experiment, I tried to align two Kinects using this method. The process is basically identical except that the extra Kinect introduces one more time colour detection and extraction process.
From the Figure 4, we can see that the result is quite good as the top side of the box is aligned without any visible error.

Figure 4 Animation that shows good alignment of point clouds from two Kinects

Reference:
[1] Microsoft Dev Centre - Color : link

Circular trajectory based on Start and End point

By knowing start and end point of a trajectory, we want to create a circular trajectory which can avoid body and provide smooth path for robot navigation.


Middle Point Generation:

A circle is unique if and only if three points are known, therefore, we need to calculate the middle point between the start and end point. As shown in Figure 1, we have two points P1 and P4 on a plane which is assumed to be parallel to table. In order to find the middle point, we artificially create two points P2 and P3 which have same x-axis offset to P4 and P1 respectively. Next, we connect P1 with P2 and P4 with P3 by which two lines are intersected. From the intersection point, we can estimate its normal and therefore create our middle point by extending the point at normal direction. Note that the normal must be upward so the trajectory will cross over body rather then go under table.

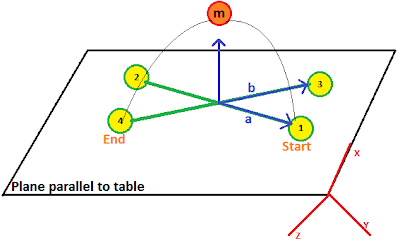Figure 1 schematic of middle point generation based on two end points

Circle calculation (centre and radius):
Let's label the start, middle and end point to 0, 1 and 2. Here is snippet for the circle calculation:

 /*
  Circle calculation algorithm refer to:
  Implementation of arc interpolation in a robot by using three arbitrary points (Chinese), Ye Bosheng, 2007
 */
 float a00, a01, a02, a10, a11, a12, a20, a21, a22, b0, b1, b2;

 // Matrix A (3x3)
 a00 = 2 * (Cstart_[0] - Cmiddle_[0]); // 2 * (X0 - X1)
 a01 = 2 * (Cstart_[1] - Cmiddle_[1]); // 2 * (Y0 - Y1)
 a02 = 2 * (Cstart_[2] - Cmiddle_[2]); // 2 * (Z0 - Z1)

 a10 = 2 * (Cmiddle_[0] - Cend_[0]);  // 2 * (X1 - X2)
 a11 = 2 * (Cmiddle_[1] - Cend_[1]);  // 2 * (Y1 - Y2)
 a12 = 2 * (Cmiddle_[2] - Cend_[2]);  // 2 * (Z1 - Z2)
 
 a20 = a02 * (a02 * a11 - a01 * a12) / 8;
 a21 = a02 * (a00 * a12 - a02 * a10) / 8;
 a22 = - (a00 * (a02 * a11 - a01 * a12) + a01 * (a00 * a12 - a02 * a10)) / 8;

 // Matrix B (3x1)
 // b0 = (X0^2 + Y0^2 + Z0^2) - (X1^2 + Y1^2 + Z1^2)
 b0 = (Cstart_[0]*Cstart_[0] + Cstart_[1]*Cstart_[1] + Cstart_[2]*Cstart_[2])
  - (Cmiddle_[0]*Cmiddle_[0] + Cmiddle_[1]*Cmiddle_[1] + Cmiddle_[2]*Cmiddle_[2]);

 // b1 = (X1^2 + Y1^2 + Z1^2) - (X2^2 + Y2^2 + Z2^2)
 b1 = (Cmiddle_[0]*Cmiddle_[0] + Cmiddle_[1]*Cmiddle_[1] + Cmiddle_[2]*Cmiddle_[2])
  - (Cend_[0]*Cend_[0] + Cend_[1]*Cend_[1] + Cend_[2]*Cend_[2]);

 // b2 = a20*X0 + a21*Y0 + a22*Z0
 b2 = a20 * Cstart_[0] + a21 * Cstart_[1] + a22 * Cstart_[2];

 Eigen::Matrix3f A;
 Eigen::Vector3f B;

 A << a00, a01, a02, 
   a10, a11, a12,
   a20, a21, a22; 
 B << b0, b1, b2;

 /* 
  Centre of circle [Xc Yc Zc] can be calculated as
  A * [Xc Yc Zc]' = B;
  For Eigen library solving Ax = b, refer to:
  http://eigen.tuxfamily.org/dox/TutorialLinearAlgebra.html
 */
 Ccentre_= A.colPivHouseholderQr().solve(B);
 
 /*
  Radius of circle can be calculated as:
  R = [(X0 - Xc)^2 + (Y0 - Yc)^2 + (Z0 - Zc)^2]^0.5
 */
 float temp_equa;
 temp_equa = (Cstart_[0] - Ccentre_[0]) * (Cstart_[0] - Ccentre_[0]);
 temp_equa += (Cstart_[1] - Ccentre_[1]) * (Cstart_[1] - Ccentre_[1]);
 temp_equa += (Cstart_[2] - Ccentre_[2]) * (Cstart_[2] - Ccentre_[2]);
 radius_ = sqrt(temp_equa);

Trajectory interpolation:
Here is the snippet for determining central angle:

 /*
  normal of circle plane
  u = (Y1 - Y0)(Z2 - Z1) - (Z1 - Z0)(Y2 - Y1)
  v = (Z1 - Z0)(X2 - X1) - (X1 - X0)(Z2 - Z1)
  w = (X1 - X0)(Y2 - Y1) - (Y1 - Y0)(X2 - X1)
 */
 Cnu_ = (Cmiddle_[1] - Cstart_[1]) * (Cend_[2] - Cmiddle_[2]) - (Cmiddle_[2] - Cstart_[2]) * (Cend_[1] - Cmiddle_[1]);
 Cnv_ = (Cmiddle_[2] - Cstart_[2]) * (Cend_[0] - Cmiddle_[0]) - (Cmiddle_[0] - Cstart_[0]) * (Cend_[2] - Cmiddle_[2]);
 Cnw_ = (Cmiddle_[0] - Cstart_[0]) * (Cend_[1] - Cmiddle_[1]) - (Cmiddle_[1] - Cstart_[1]) * (Cend_[0] - Cmiddle_[0]);

 // normal vector to determine central angle
 float u1, v1, w1;
 u1 = (Cstart_[1] - Ccentre_[1]) * (Cend_[2] - Cstart_[2]) - (Cstart_[2] - Ccentre_[2]) * (Cend_[1] - Cstart_[1]);
 v1 = (Cstart_[2] - Ccentre_[2]) * (Cend_[0] - Cstart_[0]) - (Cstart_[0] - Ccentre_[0]) * (Cend_[2] - Cstart_[2]);
 w1 = (Cstart_[0] - Ccentre_[0]) * (Cend_[1] - Cstart_[1]) - (Cstart_[1] - Ccentre_[1]) * (Cend_[0] - Cstart_[0]);

 float H, temp;
 H = Cnu_ * u1 + Cnv_ * v1 + Cnw_ * w1;
 temp = (Cend_[0] - Cstart_[0]) * (Cend_[0] - Cstart_[0]) + 
   (Cend_[1] - Cstart_[1]) * (Cend_[1] - Cstart_[1]) +
   (Cend_[2] - Cstart_[2]) * (Cend_[2] - Cstart_[2]);
 if (H >= 0) // theta <= PI
 {
  Ctheta = 2 * asin(sqrt(temp) / (2 * radius_));
 } 
 else  // theta > PI
 {
  Ctheta = 2 * M_PI - 2 * asin(sqrt(temp) / (2 * radius_));
 }

Here is the snippet for calculation of number of points to be interpolated:

int CircleGenerator::CalcNbOfPts(const float &step)
{
 float temp;
 temp = 1 + (step / radius_) * (step / radius_);
 paramG_ = 1 / sqrt(temp);

 temp = Cnu_*Cnu_ + Cnv_*Cnv_ + Cnw_*Cnw_;
 paramE_ = step / (radius_ * sqrt(temp));

 float sigma;
 sigma = step / radius_;

 int N;
 N = (int)(Ctheta / sigma) + 1;

 return (N);
}

Here is the snippet for calculating next point in the trajectory:

 traj->push_back(vector2pcl(circle_->Cstart_));
 for (int i = 1; i < numOfPt; i++)
 {
  /*
   Equation 8:
   mi = v(Zi - Zc) - w(Yi - Yc)
   ni = w(Xi - Xc) - u(Zi - Zc)
   li = u(Yi - Yc) - v(Xi - Xc)
  */
  if (i == 1)
  {
   pre = circle_->Cstart_;
  }
  float mi, ni, li;
  mi = circle_->Cnv_ * (pre[2] - circle_->Ccentre_[2]) - circle_->Cnw_ * (pre[1] - circle_->Ccentre_[1]);
  ni = circle_->Cnw_ * (pre[0] - circle_->Ccentre_[0]) - circle_->Cnu_ * (pre[2] - circle_->Ccentre_[2]);
  li = circle_->Cnu_ * (pre[1] - circle_->Ccentre_[1]) - circle_->Cnv_ * (pre[0] - circle_->Ccentre_[0]);
  
  /*
   X(i+1) = Xc + G * (X(i) + E*mi - Xc)
   Y(i+1) = Yc + G * (Y(i) + E*ni - Yc)
   Z(i+1) = Zc + G * (Z(i) + E*li - Zc)
  */
  curr[0] = circle_->Ccentre_[0] + circle_->paramG_ * (pre[0] + circle_->paramE_ * mi - circle_->Ccentre_[0]);
  curr[1] = circle_->Ccentre_[1] + circle_->paramG_ * (pre[1] + circle_->paramE_ * ni - circle_->Ccentre_[1]);
  curr[2] = circle_->Ccentre_[2] + circle_->paramG_ * (pre[2] + circle_->paramE_ * li - circle_->Ccentre_[2]);
  traj->push_back(vector2pcl(curr));
  pre = curr;
 }
 traj->push_back(vector2pcl(circle_->Cend_));

Point cloud normal estimation and Correspondence based on Normal shooting

Souce cloud: shape model

Target cloud: point cloud from Kinect

Normal cloud: a cloud of normal for shape model cloud

Step 1: Normal estimation based on point cloud itself

Step 2: Figure out the normal direction based on the view port position

Step 3: Find the correspondence in target cloud for each point in source cloud (shape model)

Results:

Figure 1 Red points: shape model cloud; Blue line: normal starts from point; colorful point: cloud from Kinect

Figure 2 Side view of Figure 1.

Figure 3 Top view of Figure 1.

Figure 4 Green points are the correspondences obtained from normal shooting

Calculating Euler angles from a rotation matrix

For rotation with inverse order Rzxy, refer to here.

Finding transformation between corresponding 3D points

With the shape model registered with point cloud, we need to align it with the mean model so that they are in same reference frame and comparable.
The transformation between shape model and mean model includes translation, scaling and rotation.

Translation:
In order to make two shape comparable, I translate both registered shape model and mean model to origin.

Scaling:
A simple way is to normalize the shape itself which results in a scaled shape of size 1. The size of shape is calculated by Opencv cv::norm() which computes an absolute array norm based on following equation.

In my program I use NORM_L2.

Rotation:
Now the registered shape model and the mean shape are almost aligned except the rotation. As the correspondences between two shape are known information, the rotation matrix can be solved using SVD (singular vector decomposition) which is introduced here.
Firstly, we need to decompose matrix H which is:

As the centroid of two shape has been subtracted already in the translation part, we can just put PA and PB as our two shapes. Next, the SVD of H is:

Finally, the rotation matrix from shape A to shape B can be calculated using U and V:

If we want to get rotation from shape B to A, just alter the equation to PB*PA instead of PA*PB.


Reference:
[1] Finding optimal rotation and translation between corresponding 3D points
[2] OpenCV document