Middle Point Generation:
A circle is unique if and only if three points are known, therefore, we need to calculate the middle point between the start and end point. As shown in Figure 1, we have two points P1 and P4 on a plane which is assumed to be parallel to table. In order to find the middle point, we artificially create two points P2 and P3 which have same x-axis offset to P4 and P1 respectively. Next, we connect P1 with P2 and P4 with P3 by which two lines are intersected. From the intersection point, we can estimate its normal and therefore create our middle point by extending the point at normal direction. Note that the normal must be upward so the trajectory will cross over body rather then go under table.
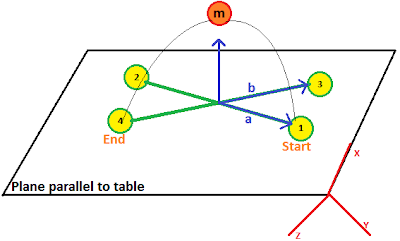 |
| Figure 1 schematic of middle point generation based on two end points |
Let's label the start, middle and end point to 0, 1 and 2. Here is snippet for the circle calculation:
/* Circle calculation algorithm refer to: Implementation of arc interpolation in a robot by using three arbitrary points (Chinese), Ye Bosheng, 2007 */ float a00, a01, a02, a10, a11, a12, a20, a21, a22, b0, b1, b2; // Matrix A (3x3) a00 = 2 * (Cstart_[0] - Cmiddle_[0]); // 2 * (X0 - X1) a01 = 2 * (Cstart_[1] - Cmiddle_[1]); // 2 * (Y0 - Y1) a02 = 2 * (Cstart_[2] - Cmiddle_[2]); // 2 * (Z0 - Z1) a10 = 2 * (Cmiddle_[0] - Cend_[0]); // 2 * (X1 - X2) a11 = 2 * (Cmiddle_[1] - Cend_[1]); // 2 * (Y1 - Y2) a12 = 2 * (Cmiddle_[2] - Cend_[2]); // 2 * (Z1 - Z2) a20 = a02 * (a02 * a11 - a01 * a12) / 8; a21 = a02 * (a00 * a12 - a02 * a10) / 8; a22 = - (a00 * (a02 * a11 - a01 * a12) + a01 * (a00 * a12 - a02 * a10)) / 8; // Matrix B (3x1) // b0 = (X0^2 + Y0^2 + Z0^2) - (X1^2 + Y1^2 + Z1^2) b0 = (Cstart_[0]*Cstart_[0] + Cstart_[1]*Cstart_[1] + Cstart_[2]*Cstart_[2]) - (Cmiddle_[0]*Cmiddle_[0] + Cmiddle_[1]*Cmiddle_[1] + Cmiddle_[2]*Cmiddle_[2]); // b1 = (X1^2 + Y1^2 + Z1^2) - (X2^2 + Y2^2 + Z2^2) b1 = (Cmiddle_[0]*Cmiddle_[0] + Cmiddle_[1]*Cmiddle_[1] + Cmiddle_[2]*Cmiddle_[2]) - (Cend_[0]*Cend_[0] + Cend_[1]*Cend_[1] + Cend_[2]*Cend_[2]); // b2 = a20*X0 + a21*Y0 + a22*Z0 b2 = a20 * Cstart_[0] + a21 * Cstart_[1] + a22 * Cstart_[2]; Eigen::Matrix3f A; Eigen::Vector3f B; A << a00, a01, a02, a10, a11, a12, a20, a21, a22; B << b0, b1, b2; /* Centre of circle [Xc Yc Zc] can be calculated as A * [Xc Yc Zc]' = B; For Eigen library solving Ax = b, refer to: http://eigen.tuxfamily.org/dox/TutorialLinearAlgebra.html */ Ccentre_= A.colPivHouseholderQr().solve(B); /* Radius of circle can be calculated as: R = [(X0 - Xc)^2 + (Y0 - Yc)^2 + (Z0 - Zc)^2]^0.5 */ float temp_equa; temp_equa = (Cstart_[0] - Ccentre_[0]) * (Cstart_[0] - Ccentre_[0]); temp_equa += (Cstart_[1] - Ccentre_[1]) * (Cstart_[1] - Ccentre_[1]); temp_equa += (Cstart_[2] - Ccentre_[2]) * (Cstart_[2] - Ccentre_[2]); radius_ = sqrt(temp_equa);
Trajectory interpolation:
Here is the snippet for determining central angle:
/*
normal of circle plane
u = (Y1 - Y0)(Z2 - Z1) - (Z1 - Z0)(Y2 - Y1)
v = (Z1 - Z0)(X2 - X1) - (X1 - X0)(Z2 - Z1)
w = (X1 - X0)(Y2 - Y1) - (Y1 - Y0)(X2 - X1)
*/
Cnu_ = (Cmiddle_[1] - Cstart_[1]) * (Cend_[2] - Cmiddle_[2]) - (Cmiddle_[2] - Cstart_[2]) * (Cend_[1] - Cmiddle_[1]);
Cnv_ = (Cmiddle_[2] - Cstart_[2]) * (Cend_[0] - Cmiddle_[0]) - (Cmiddle_[0] - Cstart_[0]) * (Cend_[2] - Cmiddle_[2]);
Cnw_ = (Cmiddle_[0] - Cstart_[0]) * (Cend_[1] - Cmiddle_[1]) - (Cmiddle_[1] - Cstart_[1]) * (Cend_[0] - Cmiddle_[0]);
// normal vector to determine central angle
float u1, v1, w1;
u1 = (Cstart_[1] - Ccentre_[1]) * (Cend_[2] - Cstart_[2]) - (Cstart_[2] - Ccentre_[2]) * (Cend_[1] - Cstart_[1]);
v1 = (Cstart_[2] - Ccentre_[2]) * (Cend_[0] - Cstart_[0]) - (Cstart_[0] - Ccentre_[0]) * (Cend_[2] - Cstart_[2]);
w1 = (Cstart_[0] - Ccentre_[0]) * (Cend_[1] - Cstart_[1]) - (Cstart_[1] - Ccentre_[1]) * (Cend_[0] - Cstart_[0]);
float H, temp;
H = Cnu_ * u1 + Cnv_ * v1 + Cnw_ * w1;
temp = (Cend_[0] - Cstart_[0]) * (Cend_[0] - Cstart_[0]) +
(Cend_[1] - Cstart_[1]) * (Cend_[1] - Cstart_[1]) +
(Cend_[2] - Cstart_[2]) * (Cend_[2] - Cstart_[2]);
if (H >= 0) // theta <= PI
{
Ctheta = 2 * asin(sqrt(temp) / (2 * radius_));
}
else // theta > PI
{
Ctheta = 2 * M_PI - 2 * asin(sqrt(temp) / (2 * radius_));
}
Here is the snippet for calculation of number of points to be interpolated:
int CircleGenerator::CalcNbOfPts(const float &step)
{
float temp;
temp = 1 + (step / radius_) * (step / radius_);
paramG_ = 1 / sqrt(temp);
temp = Cnu_*Cnu_ + Cnv_*Cnv_ + Cnw_*Cnw_;
paramE_ = step / (radius_ * sqrt(temp));
float sigma;
sigma = step / radius_;
int N;
N = (int)(Ctheta / sigma) + 1;
return (N);
}
Here is the snippet for calculating next point in the trajectory:
traj->push_back(vector2pcl(circle_->Cstart_));
for (int i = 1; i < numOfPt; i++)
{
/*
Equation 8:
mi = v(Zi - Zc) - w(Yi - Yc)
ni = w(Xi - Xc) - u(Zi - Zc)
li = u(Yi - Yc) - v(Xi - Xc)
*/
if (i == 1)
{
pre = circle_->Cstart_;
}
float mi, ni, li;
mi = circle_->Cnv_ * (pre[2] - circle_->Ccentre_[2]) - circle_->Cnw_ * (pre[1] - circle_->Ccentre_[1]);
ni = circle_->Cnw_ * (pre[0] - circle_->Ccentre_[0]) - circle_->Cnu_ * (pre[2] - circle_->Ccentre_[2]);
li = circle_->Cnu_ * (pre[1] - circle_->Ccentre_[1]) - circle_->Cnv_ * (pre[0] - circle_->Ccentre_[0]);
/*
X(i+1) = Xc + G * (X(i) + E*mi - Xc)
Y(i+1) = Yc + G * (Y(i) + E*ni - Yc)
Z(i+1) = Zc + G * (Z(i) + E*li - Zc)
*/
curr[0] = circle_->Ccentre_[0] + circle_->paramG_ * (pre[0] + circle_->paramE_ * mi - circle_->Ccentre_[0]);
curr[1] = circle_->Ccentre_[1] + circle_->paramG_ * (pre[1] + circle_->paramE_ * ni - circle_->Ccentre_[1]);
curr[2] = circle_->Ccentre_[2] + circle_->paramG_ * (pre[2] + circle_->paramE_ * li - circle_->Ccentre_[2]);
traj->push_back(vector2pcl(curr));
pre = curr;
}
traj->push_back(vector2pcl(circle_->Cend_));























